BP算法主要是用于修改神经网络的参数值的算法,主要运用到的知识是求导的链式法则,
现在现在有如下数据X是一个2行2列的矩阵,Y是我们的标签矩阵3行2列(这里的Y采取了独特码的形式由此可得数据的标签类别有三类)我们的隐藏层大小有一层,神经元的数目为2个,此时我们就可以得出我们的权值矩阵数目为我们假设他们为W^{[1]},W^{[2]},b^{[1]},b^{[2]}那么就可以的到每层神经元的输入值第一层的输入值为数据X,第二层的输入值为
Z^{[1]}=W^{[1]}\cdot{X}+b^{[1]}
(这个也可以当作是第一层的输出值)
由此可得我们第二层的输出值
A^{[1]}=\sigma(Z^{[1]})(其中可以令\sigma(x) = \frac{1}{1 + e^{-x}}也可以是其他的形式)
至此我们的前向传播就完成了我们的目的地就是使得这个损失函数的值最小由于这个函数的表达式是复合函数的所以链式法则方便了函数求导修改各个参数。
下面进入重点如何修改我们的目标值(W^{[1]},W2^{[2]},b1^{[1]},b^{[2]})。
X=\begin{bmatrix}
x_{[1]}^{(1)}&x_{[1]}^{(2)}\\
x_{[2]}^{(1)}&x_{[2]}^{(2)}\\
\end{bmatrix}
Y=\begin{bmatrix}
y_{[1]}^{(1)}&y_{[1]}^{(2)}\\
y_{[2]}^{(1)}&y_{[2]}^{(2)}\\
y_{[3]}^{(1)}&y_{[3]}^{(2)}\\
\end{bmatrix}
W1=\begin{bmatrix}
w_{[1][1]}^{(1)} & w_{[1][2]}^{(1)}\\
w_{[2][1]}^{(1)} & w_{[2][2]}^{(1)}\\
\end{bmatrix}
b1=\begin{bmatrix}
b_{[1]}^{(1)}\\
b_{[2]}^{(1)}\\
\end{bmatrix}
Z1=\begin{bmatrix}
z1_{[1]}^{(1)}&z1_{[1]}^{(2)}\\
z1_{[2]}^{(1)}&z1_{[2]}^{(2)}\\
\end{bmatrix}=W1
\cdot
X+b1=\begin{bmatrix}
w_{[1][1]}^{(1)} & w_{[1][2]}^{(1)}\\
w_{[2][1]}^{(1)} & w_{[2][2]}^{(1)}\\
\end{bmatrix}
{\cdot}
\begin{bmatrix}
x_{[1]}^{(1)}&x_{[1]}^{(2)}\\
x_{[2]}^{(1)}&x_{[2]}^{(2)}\\
\end{bmatrix}+
\begin{bmatrix}
b_{[1]}^{(1)}\\
b_{[2]}^{(1)}\\
\end{bmatrix}
A1=\begin{bmatrix}
A1_{[1]}^{(1)}&A1_{[1]}^{(2)}\\
A1_{[2]}^{(1)}&A1_{[2]}^{(2)}\\
\end{bmatrix}=
\begin{bmatrix}
\sigma(z1_{[1]}^{(1)})&\sigma(z1_{[1]}^{(2)})\\
\sigma(z1_{[2]}^{(1)})&\sigma(z1_{[2]}^{(2)})\\
\end{bmatrix}
W2=\begin{bmatrix}
w_{[1][1]}^{(2)} & w_{[1][2]}^{(2)}\\
w_{[2][1]}^{(2)} & w_{[2][2]}^{(2)}\\
w_{[3][1]}^{(2)} & w_{[3][2]}^{(2)}\\
\end{bmatrix}
b2=\begin{bmatrix}
b_{[1]}^{(2)}\\
b_{[2]}^{(2)}\\
b_{[3]}^{(2)}
\end{bmatrix}
Z2=\begin{bmatrix}
z2_{[1]}^{(1)}&z2_{[1]}^{(2)}\\
z2_{[2]}^{(1)}&z2_{[2]}^{(2)}\\
z2_{[3]}^{(1)}&z2_{[3]}^{(2)}\\
\end{bmatrix}=W^{[2]}\cdot A^{[1]}+b^{[2]}=W^{[2]}=
\begin{bmatrix}
w_{[1][1]}^{(2)} & w_{[1][2]}^{(2)}\\
w_{[2][1]}^{(2)} & w_{[2][2]}^{(2)}\\
w_{[3][1]}^{(2)} & w_{[3][2]}^{(2)}\\
\end{bmatrix}\cdot
\begin{bmatrix}
A1_{[1]}^{(1)}&A1_{[1]}^{(2)}\\
A1_{[2]}^{(1)}&A1_{[2]}^{(2)}\\
\end{bmatrix}+
\begin{bmatrix}
b_{[1]}^{(2)}\\
b_{[2]}^{(2)}\\
b_{[3]}^{(2)}
\end{bmatrix}
A2=\begin{bmatrix}
A2_{[1]}^{(1)}&A2_{[1]}^{(2)}\\
A2_{[2]}^{(1)}&A2_{[2]}^{(2)}\\
A2_{[3]}^{(1)}&A2_{[3]}^{(2)}\\
\end{bmatrix}=softmax(Z2)=
Z2=\begin{bmatrix}
softmax(z2_{[1]}^{(1)})&softmax(z2_{[1]}^{(2)})\\
softmax(z2_{[2]}^{(1)})&softmax(z2_{[2]}^{(2)})\\
softmax(z2_{[3]}^{(1)})&softmax(z2_{[3]}^{(2)})\\
\end{bmatrix}
由此可得我们需要修改的参数就是W1,W2,b1,b2这四个矩阵先从W2开始
我们要将的是dW2
dW2=\begin{bmatrix}
\frac{\partial L}{\partial w_{[1][1]}^{(1)}} &\frac{\partial L}{\partial w_{[1][2]}^{(1)}}\\
\frac{\partial L}{\partial w_{[2][1]}^{(1)}}&\frac{\partial L}{\partial w_{[2][2]}^{(1)}}\\
\end{bmatrix}
那么W2是如何变成我们的loss的呢通过上图我们可以大致看出来这一系列的链式变化:
\frac{\partial L}{\partial W2}=\frac{\partial L}{\partial A2}\frac{\partial A2}{\partial Z2}\frac{\partial Z2}{\partial W2}
由此我们可以得出我们可以根据上述的Z2的计算方式不难发现我们的w_{[1][1]}^{(2)}会出现在我们Z2矩阵的第一行中即z2_{[1]}^{(1)}=\ldots +w_{[1][1]}^{(2)}A1_{[1]}^{(1)}+\ldots \hspace{20pt} z2_{[1]}^{(2)}=\ldots +w_{[1][1]}^{(2)}A1_{[1]}^{(2)}+\ldots 又因为A2和Z2的关系是一一对应的只是对其做了一个softmax而我们的A2^{(1)}_{[1]}A2^{(1)}_{[2]}分别处于我们的L^{(1)}L^{(2)}所以我们可以得到
\frac{\partial L}{\partial w_{[1][1]}^{(2)}}=
\frac{\partial L1}{\partial w_{[1][1]}^{(2)}}+
\frac{\partial L2}{\partial w_{[1][1]}^{(2)}}=
\frac{\partial L1}{\partial A2^{(1)}_{[1]}}
\frac{\partial A2^{(1)}_{[1]}}{\partial z2_{[1]}^{(1)}}
\frac{\partial z2_{[1]}^{[1]}}{\partial w_{[1][1]}^{(2)}}+
\frac{\partial L2}{\partial A2^{(2)}_{[1]}}
\frac{\partial A2^{(2)}_{[1]}}{\partial z2_{[1]}^{(2)}}
\frac{\partial z2_{[1]}^{[2]}}{\partial w_{[1][1]}^{(2)}}
\frac{\partial L}{\partial w_{[2][1]}^{(2)}}=
\frac{\partial L1}{\partial w_{[2][1]}^{(2)}}+
\frac{\partial L2}{\partial w_{[2][1]}^{(2)}}=
\frac{\partial L1}{\partial A2^{(1)}_{[2]}}
\frac{\partial A2^{(1)}_{[2]}}{\partial z2_{[2]}^{(1)}}
\frac{\partial z2_{[2]}^{[1]}}{\partial w_{[2][1]}^{(2)}}+
\frac{\partial L2}{\partial A2^{(2)}_{[2]}}
\frac{\partial A2^{(2)}_{[2]}}{\partial z2_{[2]}^{(2)}}
\frac{\partial z2_{[2]}^{[2]}}{\partial w_{[2][1]}^{(2)}}

这里可以小小的总结一下关于W的偏导数w_{[i][j]}其中的行决定了他对应的Z所在的行数
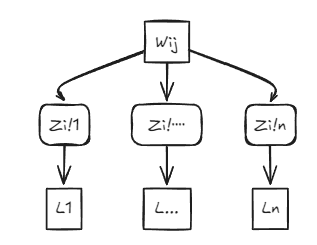
那么这个时候就可以写的很明白了
\begin{align*}
\frac{\partial z2_{[1]}^{(1)}}{\partial w_{[1][1]}^{(2)}}=A1^{(1)}_{[1]}\\
\\
\frac{\partial z2_{[1]}^{(2)}}{\partial w_{[1][1]}^{(2)}}=A1^{(2)}_{[1]}\\
\\
\frac{\partial z2_{[2]}^{[1]}}{\partial w_{[2][1]}^{(2)}}=A1^{(1)}_{[1]}\\
\\
\frac{\partial z2_{[2]}^{[2]}}{\partial w_{[2][1]}^{(2)}}=A1^{(2)}_{[1]}
\end{align*}
所以
dW2=\begin{bmatrix}
\frac{\partial L}{\partial w_{[1][1]}^{(1)}} &\frac{\partial L}{\partial w_{[1][2]}^{(1)}}\\
\frac{\partial L}{\partial w_{[2][1]}^{(1)}}&\frac{\partial L}{\partial w_{[2][2]}^{(1)}}\\
\end{bmatrix}=dZ2 \cdot A1^T
db2=\begin{bmatrix}
\frac{\partial L}{\partial b_{[1]}^{(2)}}\\
\frac{\partial L}{\partial b_{[2]}^{(2)}}\\
\frac{\partial L}{\partial b_{[3]}^{(2)}}
\end{bmatrix}
与b2相关的Z2可以写作
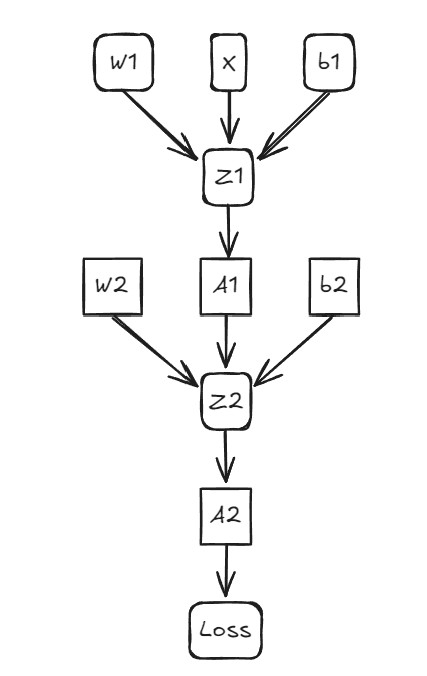
\begin{align*}
db2=\frac{\partial L}{\partial A2}\frac{\partial A2}{\partial Z2}\frac{\partial Z2}{\partial b2}\\
\frac{\partial Z2}{\partial b2}=1
\end{align*}
所以
db2=\begin{bmatrix}
\frac{\partial L}{\partial b_{[1]}^{(2)}}\\
\frac{\partial L}{\partial b_{[2]}^{(2)}}\\
\frac{\partial L}{\partial b_{[3]}^{(2)}}
\end{bmatrix}=
\begin{bmatrix}
\frac{\partial L1}{\partial A2_{[1]}^{(1)}}\frac{\partial A2_{[1]}^{(1)}}{\partial z2_{[1]}^{(1)}
}+
\frac{\partial L2}{\partial A2_{[1]}^{(2)}}\frac{\partial A2_{[1]}^{(2)}}{\partial z2_{[1]}^{(2)}}
\\
\frac{\partial L1}{\partial A2_{[2]}^{(1)}}\frac{\partial A2_{[2]}^{(1)}}{\partial z2_{[2]}^{(1)}
}+
\frac{\partial L2}{\partial A2_{[2]}^{(2)}}\frac{\partial A2_{[2]}^{(2)}}{\partial z2_{[2]}^{(2)}}
\\
\frac{\partial L1}{\partial A2_{[3]}^{(1)}}\frac{\partial A2_{[3]}^{(1)}}{\partial z2_{[3]}^{(1)}
}+
\frac{\partial L2}{\partial A2_{[3]}^{(2)}}\frac{\partial A2_{[3]}^{(2)}}{\partial z2_{[3]}^{(2)}}
\end{bmatrix}=sum(d(Z2),axis=1)
所以接下来就是W1和b1了那么关于dW1和b1其实和dW2和db2的求法很类似为什么这么说呢看看这个图你就知道了
那我们的
\begin{align*}
dW1=\frac{\partial L}{\partial A2}\frac{\partial A2}{\partial Z2}\frac{\partial Z2}{\partial A1}\frac{\partial A1}{\partial Z1}\frac{\partial Z1}{\partial W1}\\
db1=\frac{\partial L}{\partial A2}\frac{\partial A2}{\partial Z2}\frac{\partial Z2}{\partial A1}\frac{\partial A1}{\partial Z1}\frac{\partial Z1}{\partial b1}
\end{align*}
dW1=\begin{bmatrix}
\frac{\partial L}{\partial w_{[1][1]}^{(1)}} & \frac{\partial L}{\partial w_{[1][1]}^{(2)}}\\
\frac{\partial L}{\partial w_{[2][1]}^{(1)}} & \frac{\partial L}{\partial w_{[2][2]}^{(1)}}\\
\end{bmatrix}
我们先这样来理解
\frac{\partial L}{\partial w_{[1][1]}^{(1)}}=\frac{\partial L}{\partial A2}\frac{\partial A2}{\partial Z2}\frac{\partial Z2}{\partial A1}\frac{\partial A1}{\partial Z1}(\frac{\partial Z1_{[1]}^{[1]}}{\partial w_{[1][1]}^{(1)}}+\frac{\partial Z1_{[1]}^{[2]}}{\partial w_{[1][1]}^{(1)}})=\frac{\partial L}{\partial A1}\frac{\partial A1}{\partial Z1}\frac{\partial Z1}{\partial w_{[1][1]}^{(1)}}=
(
\frac{\partial L}{\partial A1_{[1]}^{(1)}}
\frac{\partial A1_{[1]}^{(1)}}{\partial Z1_{[1]}^{[1]}}
\frac{\partial Z1_{[1]}^{[1]}}{\partial w_{[1][1]}^{(1)}}+
\frac{\partial L}{\partial A1_{[1]}^{(2)}}
\frac{\partial A1_{[1]}^{(2)}}{\partial Z1_{[1]}^{[2]}}
\frac{\partial Z1_{[1]}^{[2]}}{\partial w_{[1][1]}^{(1)}})
w_{[1][2]}^{(1)}差不多
\frac{\partial L}{\partial A1_{[1]}^{(1)}}=
(\frac{\partial L1}{\partial z2_{[1]}^{(1)}}
\frac{\partial z2_{[1]}^{(1)}}{\partial A1_{[1]}^{(1)}}+
\frac{\partial L1}{\partial z2_{[2]}^{(1)}}
\frac{\partial z2_{[2]}^{(1)}}{\partial A1_{[1]}^{(1)}}+
\frac{\partial L1}{\partial z2_{[3]}^{(1)}}
\frac{\partial z2_{[3]}^{(1)}}{\partial A1_{[1]}^{(1)}})
\frac{\partial L}{\partial A1_{[1]}^{(1)}}=
(\frac{\partial L1}{\partial z2_{[1]}^{(1)}}
w_{[1][1]}^{(2)}+
\frac{\partial L1}{\partial z2_{[2]}^{(1)}}
w_{[2][1]}^{(2)}+
\frac{\partial L1}{\partial z2_{[3]}^{(1)}}
w_{[3][1]}^{(2)})
\frac{\partial L}{\partial A1_{[1]}^{(1)}}=
(\frac{\partial L1}{\partial z2_{[1]}^{(1)}}
\frac{\partial z2_{[1]}^{(1)}}{\partial A1_{[1]}^{(1)}}+
\frac{\partial L1}{\partial z2_{[2]}^{(1)}}
\frac{\partial z2_{[2]}^{(1)}}{\partial A1_{[1]}^{(1)}}+
\frac{\partial L1}{\partial z2_{[3]}^{(1)}}
\frac{\partial z2_{[3]}^{(1)}}{\partial A1_{[1]}^{(1)}})
\frac{\partial L}{\partial A1_{[1]}^{(1)}}=
(\frac{\partial L1}{\partial z2_{[1]}^{(1)}}
w_{[1][1]}^{(2)}+
\frac{\partial L1}{\partial z2_{[2]}^{(1)}}
w_{[2][1]}^{(2)}+
\frac{\partial L1}{\partial z2_{[3]}^{(1)}}
w_{[3][1]}^{(2)})
\frac{\partial L}{\partial A1_{[1]}^{(2)}}=
(\frac{\partial L2}{\partial z2_{[1]}^{(2)}}
w_{[1][2]}^{(2)}+
\frac{\partial L2}{\partial z2_{[2]}^{(2)}}
w_{[2][2]}^{(2)}+
\frac{\partial L2}{\partial z2_{[3]}^{(2)}}
w_{[3][2]}^{(2)})
dA1=W2^T\cdot Z2
(\frac{\partial L1}{\partial z2_{[1]}^{(1)}}
\frac{\partial z2_{[1]}^{(1)}}{\partial A1_{[1]}^{(1)}}+
\frac{\partial L1}{\partial z2_{[2]}^{(1)}}
\frac{\partial z2_{[2]}^{(1)}}{\partial A1_{[1]}^{(1)}}+
\frac{\partial L1}{\partial z2_{[3]}^{(1)}}
\frac{\partial z2_{[3]}^{(1)}}{\partial A1_{[1]}^{(1)}})
\frac{\partial A1_{[1]}^{(1)}}{\partial Z1_{[1]}^{[1]}}
\frac{\partial Z1_{[1]}^{[1]}}{\partial w_{[1][1]}^{(1)}}+
(\frac{\partial L2}{\partial z2_{[1]}^{(2)}}
\frac{\partial z2_{[1]}^{(1)}}{\partial A1_{[1]}^{(2)}}+
\frac{\partial L2}{\partial z2_{[2]}^{(2)}}
\frac{\partial z2_{[2]}^{(2)}}{\partial A1_{[1]}^{(2)}}+
\frac{\partial L2}{\partial z2_{[3]}^{(1)}}
\frac{\partial z2_{[3]}^{(2)}}{\partial A1_{[1]}^{(2)}}
)
\frac{\partial A1_{[1]}^{(2)}}{\partial Z1_{[1]}^{[2]}}
\frac{\partial Z1_{[1]}^{[2]}}{\partial w_{[1][1]}^{(1)}}
(\frac{\partial L1}{\partial z2_{[1]}^{(1)}}
\frac{\partial z2_{[1]}^{(1)}}{\partial A1_{[1]}^{(1)}}+
\frac{\partial L1}{\partial z2_{[2]}^{(1)}}
\frac{\partial z2_{[2]}^{(1)}}{\partial A1_{[1]}^{(1)}}+
\frac{\partial L1}{\partial z2_{[3]}^{(1)}}
\frac{\partial z2_{[3]}^{(1)}}{\partial A1_{[1]}^{(1)}}
)
\frac{\partial A1_{[1]}^{(1)}}{\partial Z1_{[1]}^{[1]}}
x_{[1]}^{(1)}+
(\frac{\partial L2}{\partial z2_{[1]}^{(2)}}
\frac{\partial z2_{[1]}^{(1)}}{\partial A1_{[1]}^{(2)}}+
\frac{\partial L2}{\partial z2_{[2]}^{(2)}}
\frac{\partial z2_{[2]}^{(2)}}{\partial A1_{[1]}^{(2)}}+
\frac{\partial L2}{\partial z2_{[3]}^{(1)}}
\frac{\partial z2_{[3]}^{(2)}}{\partial A1_{[1]}^{(2)}}
)
\frac{\partial A1_{[1]}^{(2)}}{\partial Z1_{[1]}^{[2]}}
x_{[1]}^{(2)}
这个是关于w_{[1][2]}^{(1)}
(\frac{\partial L1}{\partial z2_{[1]}^{(1)}}
\frac{\partial z2_{[1]}^{(1)}}{\partial A1_{[1]}^{(1)}}+
\frac{\partial L1}{\partial z2_{[2]}^{(1)}}
\frac{\partial z2_{[2]}^{(1)}}{\partial A1_{[1]}^{(1)}}+
\frac{\partial L1}{\partial z2_{[3]}^{(1)}}
\frac{\partial z2_{[3]}^{(1)}}{\partial A1_{[1]}^{(1)}}
)
\frac{\partial A1_{[1]}^{(1)}}{\partial Z1_{[1]}^{[1]}}
x_{[2]}^{(1)}+
(\frac{\partial L2}{\partial z2_{[1]}^{(2)}}
\frac{\partial z2_{[1]}^{(1)}}{\partial A1_{[1]}^{(2)}}+
\frac{\partial L2}{\partial z2_{[2]}^{(2)}}
\frac{\partial z2_{[2]}^{(2)}}{\partial A1_{[1]}^{(2)}}+
\frac{\partial L2}{\partial z2_{[3]}^{(1)}}
\frac{\partial z2_{[3]}^{(2)}}{\partial A1_{[1]}^{(2)}}
)
\frac{\partial A1_{[1]}^{(2)}}{\partial Z1_{[1]}^{[2]}}
x_{[2]}^{(2)}
假设前面的是一个矩阵V则dW1=V\cdot X^T=dA1*(dA1/dZ1)\cdot X^T=dZ1\cdot X^T
最后一步特别简单就是求解我们的db1了
dA1=W2^T\cdot Z2
db1=\begin{bmatrix}
\frac{\partial L}{\partial b_{[1]}^{(1)}}\\
\frac{\partial L}{\partial b_{[2]}^{(1)}}\\
\end{bmatrix}=
\begin{bmatrix}
\frac{\partial L}{\partial z1_{[1]}^{(1)}}+
\frac{\partial L}{\partial z1_{[1]}^{(2)}}\\
\frac{\partial L}{\partial z1_{[2]}^{(1)}}+
\frac{\partial L}{\partial z1_{[2]}^{(2)}}
\end{bmatrix}(sum(dZ1,axis=1))
dW1=V\cdot X^T=dA1*(dA1/dZ1)\cdot X^T=dZ1\cdot X^T
db2=\begin{bmatrix}
\frac{\partial L}{\partial b_{[1]}^{(2)}}\\
\frac{\partial L}{\partial b_{[2]}^{(2)}}\\
\frac{\partial L}{\partial b_{[3]}^{(2)}}
\end{bmatrix}=
\begin{bmatrix}
\frac{\partial L1}{\partial A2_{[1]}^{(1)}}\frac{\partial A2_{[1]}^{(1)}}{\partial z2_{[1]}^{(1)}
}+
\frac{\partial L2}{\partial A2_{[1]}^{(2)}}\frac{\partial A2_{[1]}^{(2)}}{\partial z2_{[1]}^{(2)}}
\\
\frac{\partial L1}{\partial A2_{[2]}^{(1)}}\frac{\partial A2_{[2]}^{(1)}}{\partial z2_{[2]}^{(1)}
}+
\frac{\partial L2}{\partial A2_{[2]}^{(2)}}\frac{\partial A2_{[2]}^{(2)}}{\partial z2_{[2]}^{(2)}}
\\
\frac{\partial L1}{\partial A2_{[3]}^{(1)}}\frac{\partial A2_{[3]}^{(1)}}{\partial z2_{[3]}^{(1)}
}+
\frac{\partial L2}{\partial A2_{[3]}^{(2)}}\frac{\partial A2_{[3]}^{(2)}}{\partial z2_{[3]}^{(2)}}
\end{bmatrix}=sum(d(Z2),axis=1)
dW2=\begin{bmatrix}
\frac{\partial L}{\partial w_{[1][1]}^{(1)}} &\frac{\partial L}{\partial w_{[1][2]}^{(1)}}\\
\frac{\partial L}{\partial w_{[2][1]}^{(1)}}&\frac{\partial L}{\partial w_{[2][2]}^{(1)}}\\
\end{bmatrix}=dZ2 \cdot A1^T
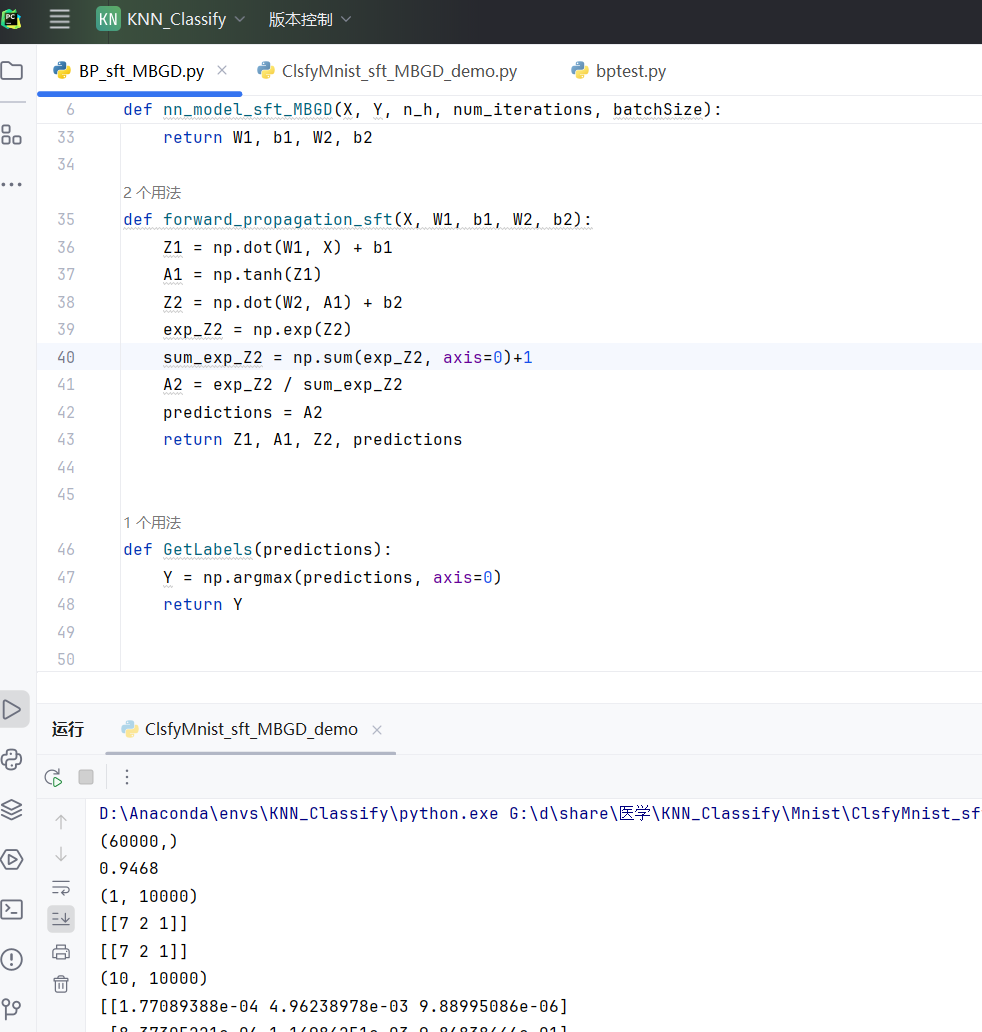
def backpropagation_sft(X, Y,W2,A1, predictions):
# 计算预测值和实际值之间的误差):
m = X.shape[1] # 假设m是样本数量
dZ2 = predictions - Y
dW2 = (1 / m) * np.dot(dZ2, A1.T)
db2 = (1 / m) * (np.sum(dZ2, axis=1))
dA1 = np.dot(W2.T,dZ2)
dZ1 = np.multiply(dA1,(1 - np.multiply(A1, A1)))
dW1 = (1 / m) * np.dot(dZ1, X.T)
db1 = (1 / m) * (np.sum(dZ1, axis=1))
return (dW1, db1, dW2, db2)








评论区